Les approximants hexagonaux métalliques aident à combler le fossé entre les quasicristaux et les structures modulées

Pendant longtemps, les scientifiques ont associé les structures cristallines à un agencement ordonné d’atomes selon un motif répétitif en forme de treillis, estimant qu’il s’agissait de la configuration la plus stable. Cependant, dans les années 1960, les progrès de la cristallographie ont révélé des matériaux qui ne correspondaient pas au modèle traditionnel. Ces structures présentent un motif non périodique ou non répétitif et sont appelées cristaux apériodiques.

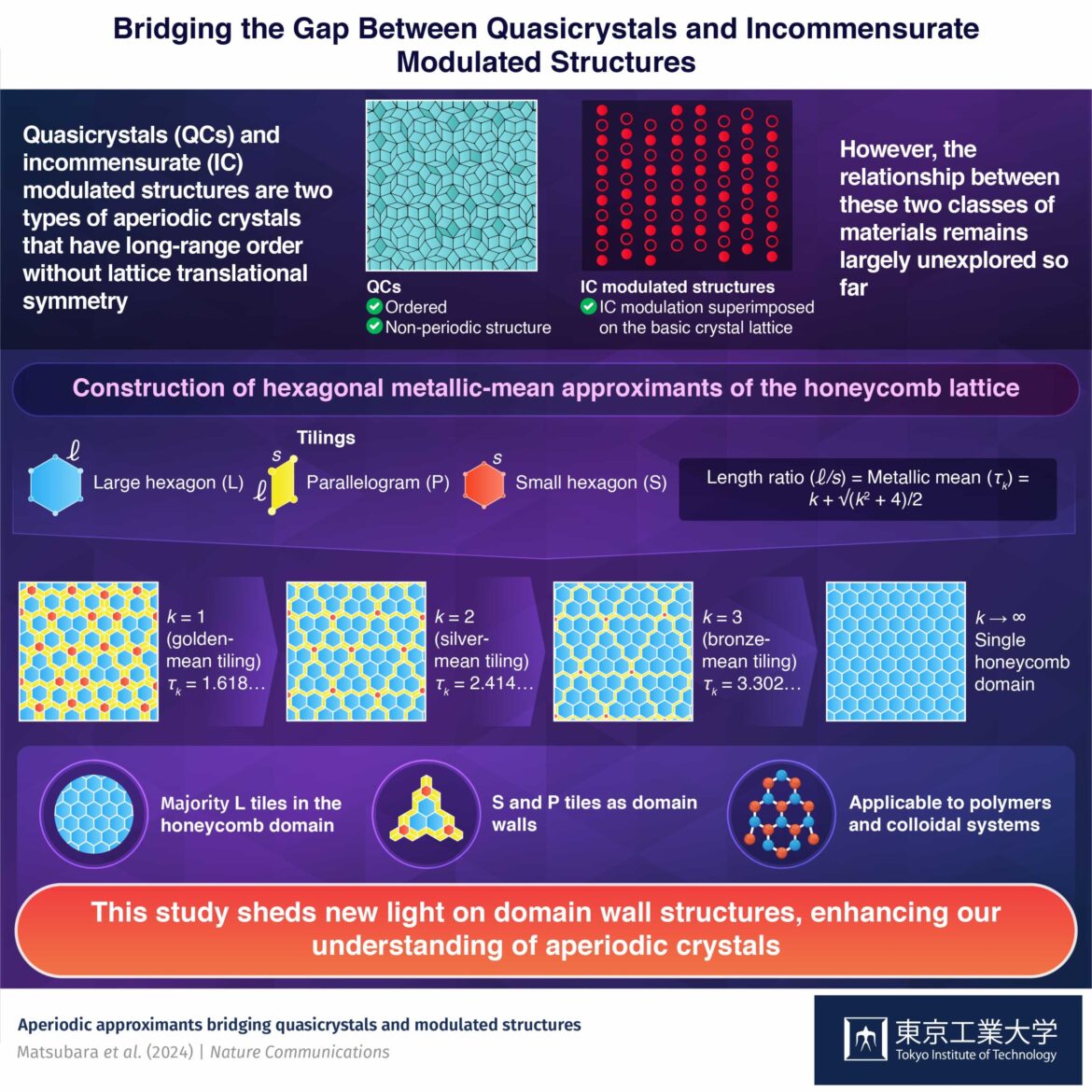
Il existe deux types de cristaux apériodiques : les quasicristaux (QC), qui présentent des arrangements ordonnés mais apériodiques, et les structures modulées de manière incommensurable (IC), où une structure de réseau périodique tridimensionnelle est déformée par des variations spatiales ou des modulations. Ces matériaux possèdent des propriétés distinctes de celles des cristaux périodiques ordinaires, mais la relation entre eux reste largement inexplorée.

Dans une étude publiée dans la revue Nature Communicationsdes chercheurs dirigés par le professeur associé Akihisa Koga du département de physique de l’Institut de technologie de Tokyo ont construit une structure en nid d’abeilles périodique locale. Ils ont disposé des tuiles hexagonales petites (S) et grandes (L) ainsi que des tuiles en parallélogramme (P) dans un espace bidimensionnel selon des moyens métalliques (généralisations des nombres d’or et d’argent bien connus), en introduisant des modulations pour générer un motif de pavage en nid d’abeilles représentant une structure modulée de manière incommensurable.

« Nous présentons des approximants hexagonaux métalliques moyens du réseau en nid d’abeille, qui comblent le fossé entre les quasicristaux et les structures modulées de manière incommensurable », explique Koga.

L’apériodicité est étroitement liée à la distance entre les positions atomiques dans le réseau cristallin. Dans les quasicristaux, ces distances sont définies comme des nombres irrationnels verrouillés par des échelles à deux longueurs, alors que dans les structures modulées par IC, elles ne sont pas fixes.

Les chercheurs ont appliqué une approximation apériodique pour organiser les pavages dans le réseau cristallin. Ils ont fait varier l’irrationnel caractéristique du réseau en fonction des moyennes métalliques, telles que la moyenne d’or, la moyenne d’argent et la moyenne de bronze. Plus précisément, ils ont organisé les tuiles de manière à ce que le rapport entre la longueur longue (représentant la taille du grand hexagone) et la longueur courte (basée sur le côté du petit hexagone et la tuile en parallélogramme) corresponde à différentes moyennes métalliques.

Au départ, l’agencement des tuiles en prenant le nombre d’or comme rapport de longueur a donné lieu à de grandes tuiles hexagonales délimitées par des parallélogrammes et à des tuiles hexagonales plus petites, créant une structure quasicristalline ordonnée mais non périodique. Cependant, à mesure que le rapport de moyenne métallique a augmenté, les tuiles hexagonales plus grandes ont commencé à se rassembler, formant des domaines en nid d’abeille, considérés comme une structure modulée par CI.

Les chercheurs ont identifié le motif de mosaïque métallique dans les polymères en utilisant un terpolymère tribloc ISP (I : polyisoprène, S : polystyrène et P : poly(2-vinylpyridine)). À partir des images du polymère prises au microscope électronique à transmission, ils ont observé que les arrangements de polymères pouvaient être représentés par des mosaïques L, P et S avec une région régulière de mosaïques L au centre et des mosaïques P à sa gauche. Les mosaïques P ont été interprétées comme des limites jumelles marquant les transitions entre différentes orientations des mosaïques L.

Ce motif de pavage a également été observé dans les particules colloïdales. Les chercheurs ont simulé le comportement de 10 000 particules colloïdales interagissant avec un potentiel de Lennard-Jones-Gauss, et ont découvert que la disposition idéale des particules est un pavage métallique moyen, constitué de triangles haut et bas.

« Notre étude met en évidence l’efficacité des approximants apériodiques pour induire des modulations au sein de systèmes de matière molle auto-assemblés utilisant le groupe de plans P31m. Plus précisément, nous avons utilisé les rangées de tuiles P comme limites de domaine dans le réseau en nid d’abeille, reliant ainsi les QC hexagonaux à moyenne métallique et les réseaux en nid d’abeille modulés IC », explique Koga.

« Ces résultats apportent un éclairage sur le domaine des cristaux apériodiques et sur leurs implications plus larges pour les structures de parois de domaine dans divers domaines. »