Crédit : Maximilien Brice : CERN
Les scientifiques ont utilisé la géométrie algébrique computationnelle pour étudier les prédictions d'expériences de physique des particules, telles que celles du Grand collisionneur de hadrons (LHC), qui a détecté pour la première fois la particule de Higgs en 2012.
Ces expériences, combinées à de nouveaux outils mathématiques, aident à résoudre beaucoup plus rapidement des questions de physique restées sans réponse et ont un impact profond sur notre compréhension de la nature. Les résultats de l'équipe ont été publiés dans Lettres d'examen physique en mars. L'équipe de recherche comprend Sebastian Mizera, membre de l'École des sciences naturelles, et ses collaborateurs Claudia Fevola (Université Paris-Saclay, Inria) et Simon Telen (Institut Max Planck de mathématiques dans les sciences),
“Nos progrès ont été rendus possibles grâce à l'utilisation d'outils récemment développés en géométrie algébrique computationnelle”, a déclaré Mizera, qui termine cet été son mandat de cinq ans à l'IAS. “C'est un exemple rare où l'utilisation d'outils mathématiques de pointe a un impact direct sur les calculs pratiques en physique des particules.”
Lorsqu’ils étudient les collisions de particules, les physiciens cherchent à décrire la probabilité que les particules arrivent à certains états : si elles se traversent, se transforment ou se dispersent sous différents angles, par exemple. Cela leur permet d’identifier de nouvelles particules ou de classer les caractéristiques de celles existantes. Pour ce faire, ils doivent étudier les interactions entre particules au niveau quantique.
Cependant, en théorie quantique, il est impossible de prédire avec certitude les conséquences d’une collision de particules. Au lieu de cela, les physiciens calculent des « amplitudes de diffusion », qui sont des expressions mathématiques qui codent la probabilité que différents résultats possibles se produisent lorsque des particules interagissent ou entrent en collision. L'une des caractéristiques que les physiciens recherchent dans ces amplitudes sont leurs « singularités », qui sont des points ou des régions où les amplitudes de probabilité deviennent infinies ou indéfinies.
Dans leur article, Mizera et ses collègues ont utilisé des outils mathématiques, notamment la topologie, la géométrie et l'algèbre, pour mieux comprendre un type particulier de singularité, à savoir les singularités de Landau. Les singularités de Landau sont des objets géométriques qui quantifient le moment où les particules virtuelles (celles limitées par le principe d'incertitude) deviennent des particules observables.
En comprenant les implications des singularités de Landau, les physiciens peuvent identifier les échelles d'énergie et les régimes cinématiques dans lesquels de nouveaux phénomènes, tels que la production de nouvelles particules, peuvent devenir possibles. Cela joue un rôle important dans l’interprétation et la réalisation de prédictions pour les expériences.
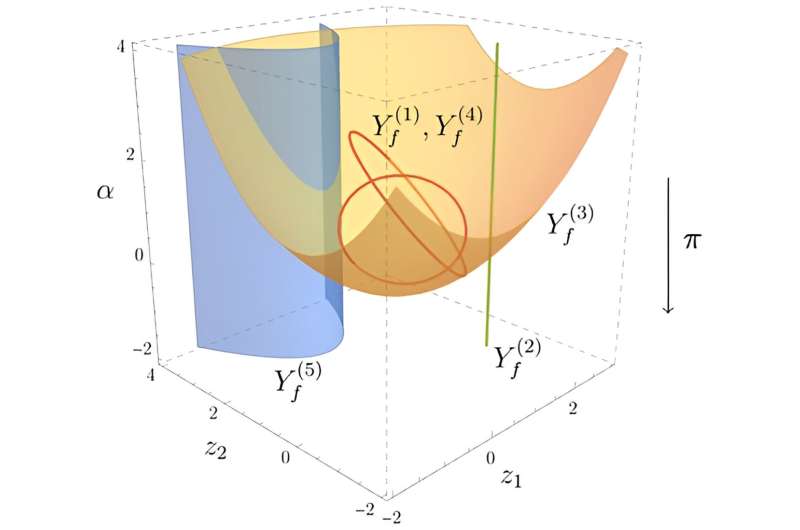
Une représentation des singularités de Landau, décrites par des équations algébriques. Crédit : Institut d’études avancées
Une variété algébrique appelée « déterminant principal de Landau », introduite par Mizera et ses collaborateurs dans leur article, est susceptible d'être encore plus utile à cet égard. La principale variante de Landau trouve des singularités même en présence de particules sans masse.
C’est significatif : localiser des singularités en présence de particules sans masse est à la fois le cas le plus important pour comprendre la physique du LHC et le plus difficile à calculer d’un point de vue mathématique.
Cette capacité a été démontrée dans l'article à l'aide d'un certain nombre d'exemples, notamment de calculs nécessaires pour comprendre la production de bosons de Higgs en présence de fortes forces nucléaires.
Il s’agit d’une étape majeure dans les progrès en cours réalisés par les physiciens du monde entier pour accroître la capacité de calcul de haute précision utilisée pour vérifier les prédictions du modèle standard de physique des particules au LHC. Les physiciens théoriciens comme Mizera et ses collaborateurs constituent une pièce essentielle de ce puzzle de particules.
Plus d'information:
Claudia Fevola et al, Les singularités de Landau revisitées : géométrie algébrique computationnelle pour les intégrales de Feynman, Lettres d'examen physique (2024). DOI : 10.1103/PhysRevLett.132.101601
Fourni par l'Institut d'études avancées
Citation: Les mathématiques de pointe fournissent un nouvel outil pour le puzzle des collisions de particules (7 juin 2024) récupéré le 7 juin 2024 sur
Ce document est soumis au droit d'auteur. En dehors de toute utilisation équitable à des fins d'étude ou de recherche privée, aucune partie ne peut être reproduite sans autorisation écrite. Le contenu est fourni seulement pour information.

